Dzielenie kątów

Wiemy, ze kąt jest to część płaszczyzny, która jest ograniczona przez dwie półproste wychodzące z jednego punktu, zwanego wierzchołkiem kąta. Każdy dowolny kąt można podzielić na połowy. W tym celu z punktu A zataczamy dowolnym promieniem łuk, który przetnie ramiona kąta w punktach B i C. Z otrzymanych punktów promieniem większym od połowy łuku BC zakreślamy łuki, które wyznaczą punkt D. Łącząc punkt D z punktem wierzchołkowym A otrzymamy prostą AD, zwaną dwusieczną kąta, która dzieli go na dwie równe części (rysunek).

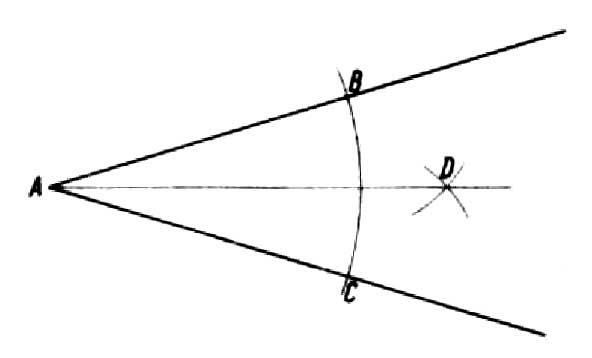
Kąt prosty dzielimy na połowy w ten sam sposób (rysunek a). Chcąc podzielić kąt prosty na trzy równe części należy z wierzchołka A dowolnym promieniem zakreślić łuk, aż do przecięcia się z ramionami kąta w punktach B i C. Tym samym promieniem z punktów B i C zakreślamy łuki, które wyznaczą punkty D i E. Łącząc je z wierzchołkiem A otrzymamy trzy kąty równe, każdy po 30 (rysunek b).

W podobny sposób można dzielić kąty na 4, 6, 8 równych części, bez posługiwania się kątomierzem. W szczególnych przypadkach, gdy stosujemy wykreślanie lub podział kątów na dowolną liczbę równych lub różnych części, posługujemy się dokładnym kątomierzem.

Kąt 60° wykreślamy w następujący sposób: Z punktu A położonego na prostej p zataczamy dowolnym promieniem luk, który przetnie tę prostą w punkcie B i z tego punktu, tym samym promieniem, zataczamy nowy łuk, który przetnie się z poprzednim w punkcie C. Łączymy punkty C i A w ten sposób otrzymujemy kąt BAC równy 60° (rysunek a).

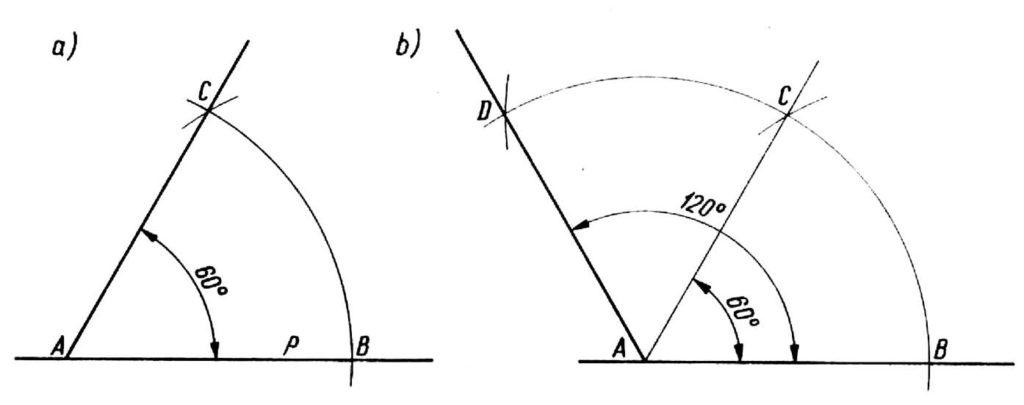
Kąt 120° wykreślamy w podobny sposób, przedłużając łuk BC i zataczając tym samym promieniem drugi łuk, który wyznaczy punkt D, Łącząc punkt A z punktem D otrzymamy żądany kąt DAB równy 120 (rysunek b). O poprawności konstrukcji można przekonać się sprawdzając wartość kąta kątomierzem lub trójkątem.