dividir ángulos

Sabemos, que el ángulo es parte del plano, que está acotado por dos rayos que parten de un punto, llamado vértice del ángulo. Cualquier ángulo arbitrario se puede dividir en mitades.. Para este propósito, desde el punto A dibujamos un arco con cualquier radio, que corta a los lados del ángulo en los puntos B y C. A partir de los puntos obtenidos con un radio mayor que la mitad del arco BC, dibujamos arcos, que determinará el punto D. Conectando el punto D con el vértice A obtenemos la recta AD, llamada la bisectriz del ángulo, que lo divide en dos partes iguales (dibujo).

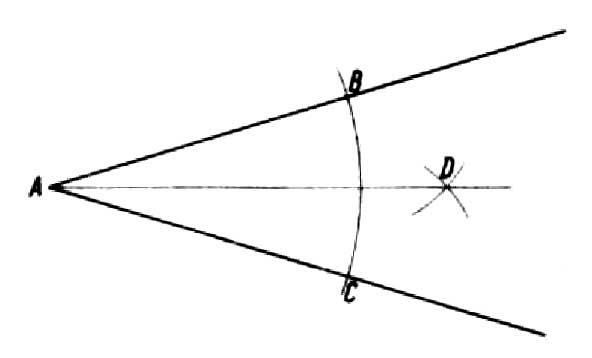
Dividimos el ángulo recto de la misma manera (figura un). Si desea dividir un ángulo recto en tres partes iguales, se debe dibujar un arco desde el vértice A con cualquier radio, hasta que se intersecan con los brazos del ángulo en los puntos B y C. Con el mismo radio desde los puntos B y C dibujamos arcos, que estará marcado por los puntos D y E. Combinándolos con el vértice A, obtenemos tres ángulos iguales, cada uno después 30 (dibujo b).

Del mismo modo, puedes dividir los ángulos en 4, 6, 8 a partes iguales, sin usar un transportador. En casos especiales, cuando usamos trazar o dividir ángulos en cualquier número de partes iguales o diferentes, usamos un transportador preciso.

Trazamos el ángulo de 60° de la siguiente manera: Desde el punto A en la línea p, rodeamos los espacios en cualquier radio, que cruzará esa línea en el punto B y desde ese punto, el mismo radio, hacemos un nuevo arco, el cual se cortará con el anterior en el punto C.. Conectamos los puntos C y A de esta manera obtenemos el ángulo BAC igual a 60° (figura un).

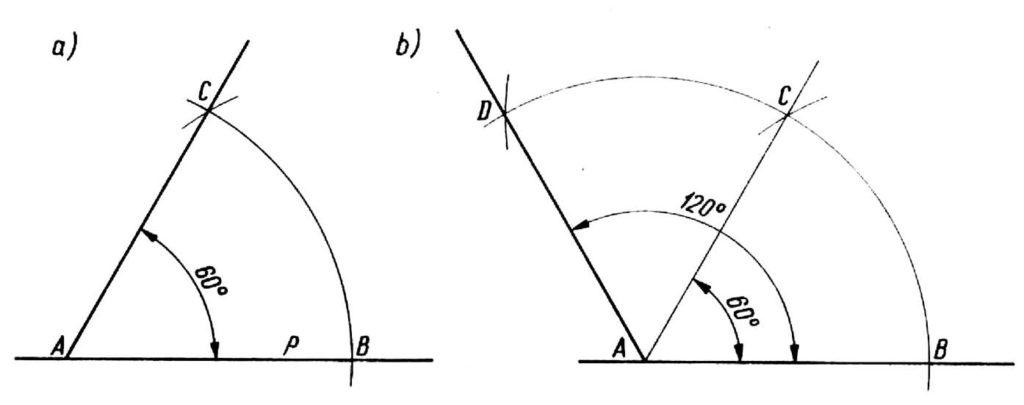
Trazamos el ángulo 120° de manera similar, extendiendo el arco BC y rodeando el segundo arco con el mismo radio, que determinará el punto D, Conectando el punto A con el punto D obtenemos el ángulo deseado DAB igual a 120 (dibujo b). Puede verificar la corrección de la construcción verificando el valor del ángulo con un transportador o un triángulo.