Delningsvinklar

Vi vet, att vinkeln är en del av planet, som begränsas av två strålar som kommer från en punkt, kallas vinkelns spets. Vilken vinkel som helst kan delas upp i halvor. För att göra detta, gör en båge med valfri radie från punkt A, som kommer att skära vinkelbenen vid punkterna B och C. Från de erhållna punkterna ritar vi bågar med en radie som är större än hälften av BC-bågen, som kommer att markera punkten D.. Förbinder vi punkten D med spetspunkten A får vi linjen AD, kallas vinkelns bisektrik, som delar den i två lika delar (teckning).

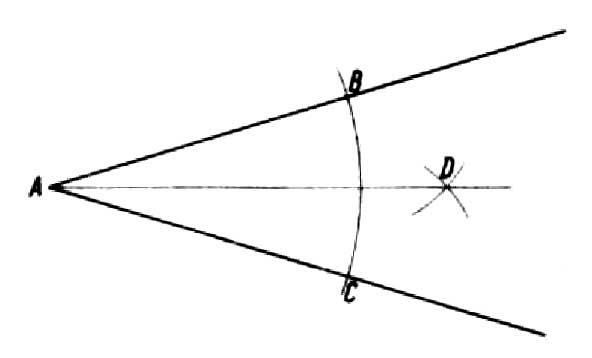
Vi delar den räta vinkeln på samma sätt (figur a). Om du vill dela en rät vinkel i tre lika delar, ska en båge ritas från vertex A med valfri radie, tills de korsar vinkelarmarna vid punkterna B och C. Med samma radie från punkterna B och C ritar vi bågar, som kommer att markeras av punkterna D och E. Genom att kombinera dem med vertex A får vi tre lika stora vinklar, varje efter 30 (ritning b).

På samma sätt kan du dela in vinklarna i 4, 6, 8 lika delar, utan att använda en gradskiva. I särskilda fall, när vi använder plotta eller dividera vinklar i valfritt antal lika eller olika delar, vi använder en korrekt gradskiva.

Vi plottar 60°-vinkeln enligt följande: Från punkt A på linjen p, ringer vi in ​​mellanrummen i valfri radie, som kommer att korsa den linjen vid punkt B och från den punkten, samma radie, vi gör en ny båge, som kommer att skära med den föregående i punkt C.. Vi kopplar ihop punkterna C och A på detta sätt får vi vinkeln BAC lika med 60° (figur a).

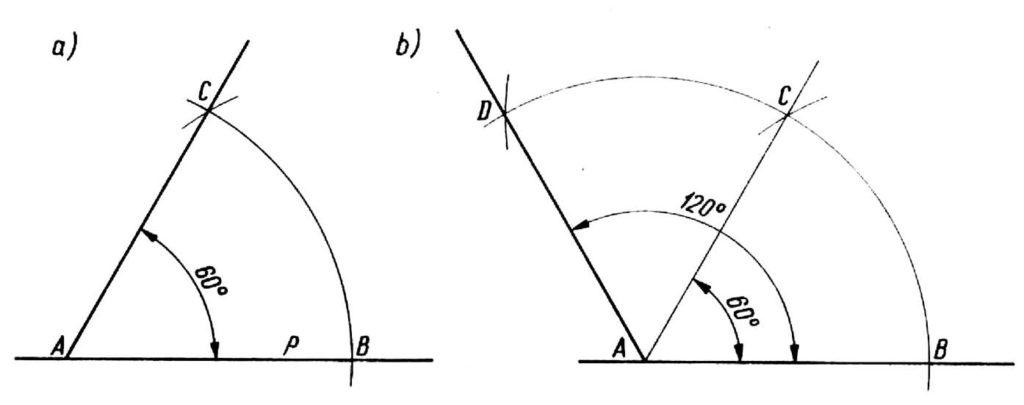
Vi plottar vinkeln 120 ° på ett liknande sätt, sträcker ut bågen BC och omger den andra bågen med samma radie, som kommer att avgöra punkt D, Förbinder vi punkt A med punkt D får vi den önskade vinkeln DAB lika med 120 (ritning b). Du kan kontrollera konstruktionens riktighet genom att kontrollera vinkelns värde med en gradskiva eller en triangel.