Jakokulmat

Me tiedämme, että kulma on osa tasoa, jota rajoittaa kaksi yhdestä pisteestä tulevaa sädettä, jota kutsutaan kulman kärjeksi. Mikä tahansa kulma voidaan jakaa puoliksi. Tee tämä tekemällä minkä tahansa säteen kaari pisteestä A, joka leikkaa kulman haarat pisteissä B ja C. Saatuista pisteistä piirretään kaaria, joiden säde on suurempi kuin puolet BC-kaaresta, joka merkitsee pisteen D.. Yhdistämällä pisteen D kärkipisteeseen A saadaan suora AD, kutsutaan kulman puolittajaksi, joka jakaa sen kahteen yhtä suureen osaan (piirustus).

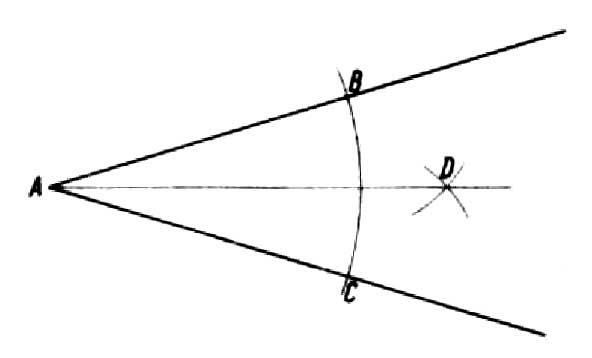
Jaamme oikean kulman samalla tavalla (kuva a). Jos halutaan jakaa suora kulma kolmeen yhtä suureen osaan, tulee kärjestä A vetää kaari millä tahansa säteellä, kunnes ne leikkaavat kulman haarat pisteissä B ja C. Samalla säteellä pisteistä B ja C piirretään kaaria, joka on merkitty pisteillä D ja E. Yhdistämällä ne kärjen A kanssa, saadaan kolme yhtäläistä kulmaa, jokaisen jälkeen 30 (piirustus b).

Samalla tavalla voit jakaa kulmat 4, 6, 8 yhtä suuret osat, ilman astemittaria. Erikoistapauksissa, kun käytämme piirtämistä tai kulmien jakamista mihin tahansa määrään yhtä suuria tai eri osia, käytämme tarkkaa astetta.

Piirrämme 60 ° kulman seuraavasti: Suoran p pisteestä A kierretään raot millä tahansa säteellä, joka ylittää kyseisen linjan pisteessä B ja siitä pisteestä, sama säde, teemme uuden kaaren, joka leikkaa edellisen pisteen C kanssa.. Yhdistämme pisteet C ja A tällä tavalla, jolloin saadaan kulma BAC, joka on yhtä suuri kuin 60 ° (kuva a).

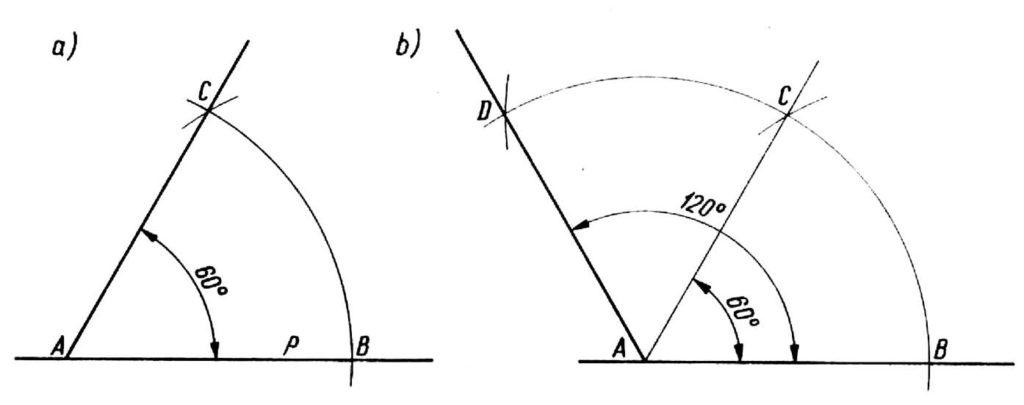
Piirrämme 120 °:n kulman samalla tavalla, pidentämällä BC-kaarta ja tekemällä sama säde toiselle kaarelle, joka määrittää pisteen D, Yhdistämällä pisteen A pisteeseen D saadaan haluttu kulma DAB, joka on yhtä suuri 120 (piirustus b). Voit tarkistaa rakenteen oikeellisuuden tarkistamalla kulman arvon astelevyllä tai kolmiolla.