Dividing angles
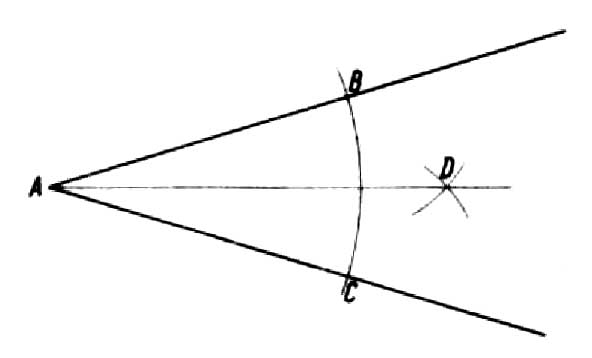
We know, that the angle is part of the plane, which is bounded by two rays coming from one point, called the vertex of the angle. Any angle can be divided into halves. To do this, we make an arc of any radius from point A, which will intersect the legs of the angle at points B and C. From the obtained points, we draw arcs with a radius greater than the half of the BC arc, which will mark point D.. Connecting the point D with the vertex point A we get the line AD, called the bisector of the angle, which divides it into two equal parts (drawing).
We divide the right angle in the same way (figure a). If you want to divide a right angle into three equal parts, an arc should be drawn from the vertex A with any radius, until they intersect with the arms of the angle at points B and C. With the same radius from points B and C we draw arcs, which will be marked by points D and E. Combining them with vertex A, we get three equal angles, each after 30 (drawing b).

Similarly, you can divide the angles into 4, 6, 8 equal parts, without using a protractor. In special cases, when we apply the plotting or division of angles into any number of equal or different parts, we use an accurate protractor.
The angle of 60° is drawn as follows: From a point A on the line p, we trace arcs with an arbitrary radius, that will intersect this line at point B and from that point, the same radius, we draw a new arc, which intersects the previous one at point C. We connect the points C and A in this way we get the angle BAC equal to 60° (figure a).
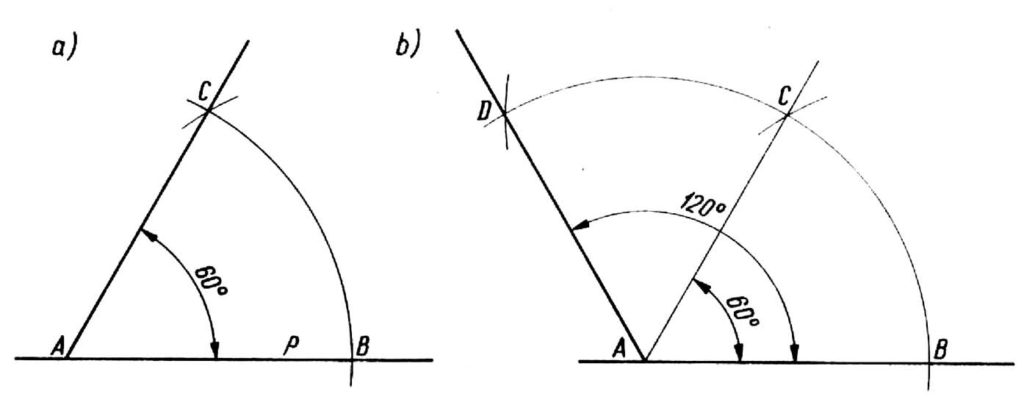
We plot the angle 120° in a similar way, extending the BC arc and making the same radius of the second arc, which will determine point D, Connecting point A with point D we get the desired angle DAB equal to 120 (drawing b). You can check the correctness of the construction by checking the angle value with a protractor or a triangle.