Angoli di divisione
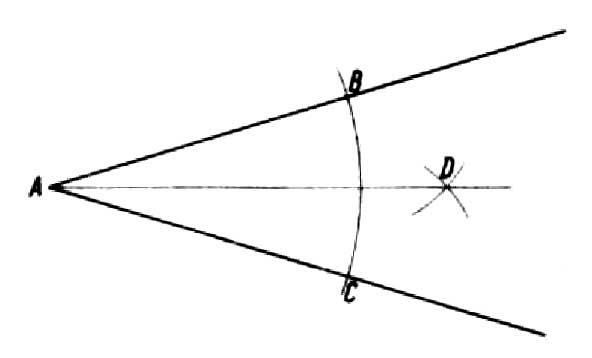
Sappiamo, che l'angolo fa parte del piano, che è delimitato da due raggi provenienti da un punto, detto vertice dell'angolo. Qualsiasi angolo arbitrario può essere diviso a metà. A tale scopo, dal punto A disegniamo un arco con qualsiasi raggio, che interseca i lati dell'angolo nei punti B e C. Dai punti ottenuti con un raggio maggiore della metà dell'arco BC, disegniamo archi, che determinerà il punto D. Collegando il punto D con il punto vertice A otteniamo la retta AD, detta bisettrice dell'angolo, che lo divide in due parti uguali (disegno).
Dividiamo l'angolo retto allo stesso modo (figura a). Se vuoi dividere un angolo retto in tre parti uguali, devi tracciare un arco dal vertice A con qualsiasi raggio, finché non si intersecano con i bracci dell'angolo nei punti B e C. Con lo stesso raggio dai punti B e C disegniamo archi, che sarà contrassegnato dai punti D ed E. Combinandoli con il vertice A, otteniamo tre angoli uguali, ciascuno dopo 30 (disegno b).

Allo stesso modo, puoi dividere gli angoli in 4, 6, 8 parti uguali, senza usare un goniometro. In casi speciali, quando usiamo il tracciamento o la divisione degli angoli in un numero qualsiasi di parti uguali o diverse, utilizziamo un goniometro accurato.
Tracciamo l'angolo di 60° come segue: Dal punto A sulla linea p, circondiamo gli spazi vuoti in qualsiasi raggio, che attraverserà quella linea nel punto B e da quel punto, lo stesso raggio, creiamo un nuovo arco, che si intersecherà con il precedente al punto C.. Colleghiamo i punti C e A in questo modo otteniamo l'angolo BAC pari a 60° (figura a).
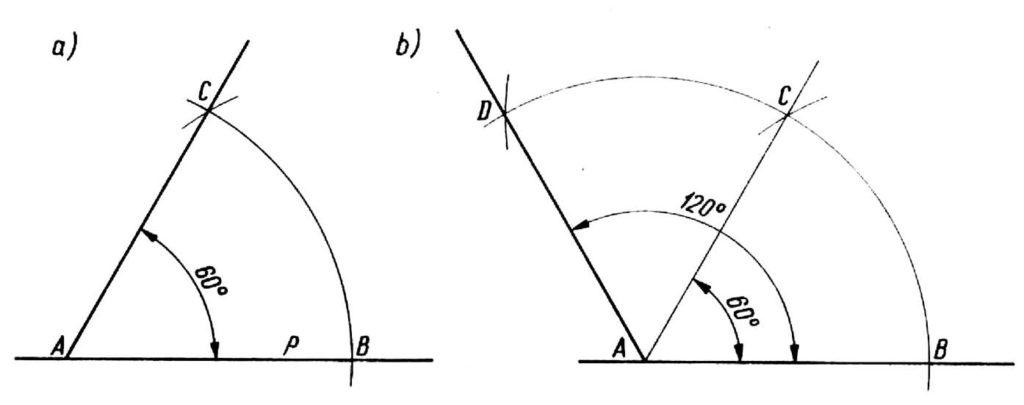
Tracciamo l'angolo di 120° in modo simile, estendendo l'arco BC e facendo lo stesso raggio del secondo arco, che determinerà il punto D, Collegando il punto A con il punto D otteniamo l'angolo desiderato DAB uguale a 120 (disegno b). È possibile verificare la correttezza della costruzione controllando il valore dell'angolo con un goniometro o un triangolo.