Angles de division
Nous savons, que l'angle fait partie du plan, qui est délimité par deux rayons provenant d'un même point, appelé sommet de l'angle. Tout angle peut être divisé en deux. Pour ce faire, faites un arc de n'importe quel rayon à partir du point A, qui coupera les branches de l'angle aux points B et C. A partir des points obtenus, on trace des arcs de rayon supérieur à la moitié de l'arc BC, qui marquera le point D.. En reliant le point D au sommet A, on obtient la droite AD, appelée bissectrice de l'angle, qui le divise en deux parties égales (dessin).
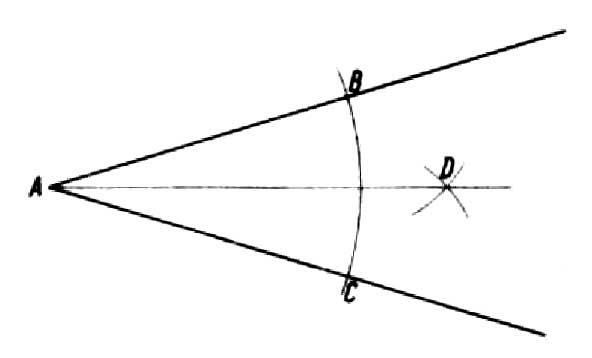
On divise l'angle droit de la même manière (figurer un). Si vous voulez diviser un angle droit en trois parties égales, un arc doit être tracé à partir du sommet A avec n'importe quel rayon, jusqu'à ce qu'ils se croisent avec les bras de l'angle aux points B et C. Avec le même rayon des points B et C, nous dessinons des arcs, qui sera marqué par les points D et E. En les combinant avec le sommet A, on obtient trois angles égaux, chacun après 30 (dessin b).

De même, vous pouvez diviser les angles en 4, 6, 8 parts égales, sans utiliser de rapporteur. Dans des cas particuliers, lorsque nous utilisons le traçage ou la division des angles en un nombre quelconque de parties égales ou différentes, nous utilisons un rapporteur précis.
Nous traçons l'angle de 60 ° comme suit: À partir du point A sur la ligne p, nous encerclons les espaces dans n'importe quel rayon, qui traversera cette ligne au point B et à partir de ce point, le même rayon, nous faisons un nouvel arc, qui se croisera avec la précédente au point C.. On relie les points C et A de cette façon on obtient l'angle BAC égal à 60° (figurer un).
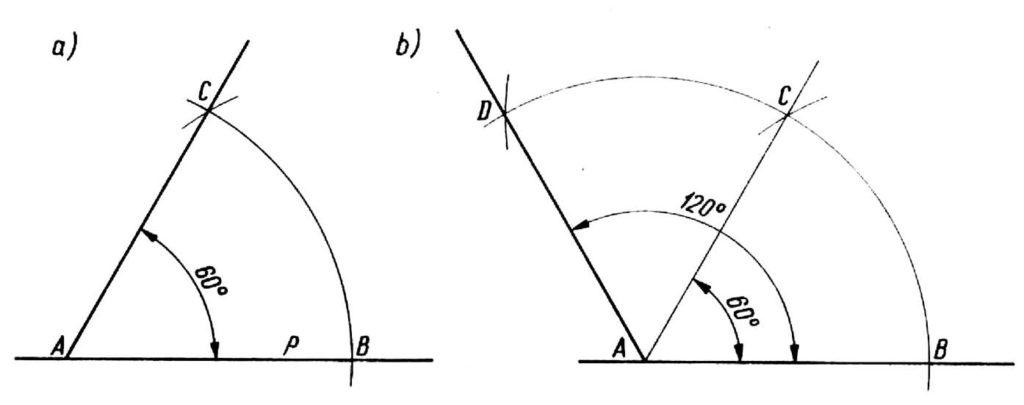
Nous traçons l'angle de 120 ° de la même manière, prolongeant l'arc BC et faisant le même rayon du deuxième arc, qui déterminera le point D, En reliant le point A au point D, nous obtenons l'angle souhaité DAB égal à 120 (dessin b). Vous pouvez vérifier l'exactitude de la construction en vérifiant la valeur de l'angle avec un rapporteur ou un triangle.